Elliptic Curve Cryptography (ECC) has grown to be very popular in public-key cryptographic systems, most popularly used in Bitcoin. ECC is based on the algebraic structures of elliptic curves over finite fields and the complexity of the elliptic curves discrete logarithm problem.
ECC incorporates all important asymmetric cryptographic systems features, including encryption, signatures, and key exchange. Because ECC employs fewer keys and signatures for the same degree of security as RSA and enables very quick key generation, key agreement, and signatures, it is considered a natural contemporary successor to the RSA cryptographic systems.
This article aims to explain elliptic curve cryptography and digital signatures used in Bitcoin in detail as simply as possible.
Public Key Cryptography
Public key cryptography or asymmetric cryptography is a cryptographic system made up of several different mathematical functions. Using a pair of keys, private and public, a person is able to encrypt any message using the intended receiver’s public key, such that the encrypted message can only be decrypted with the receiver’s private key.
private key: A value that is randomly generated and must be known only to the person that generated it. In Bitcoin, a private key is an unsigned 256 bit integer used to allow someone to spend the funds corresponding to that private key.
public key: A value that corresponds to the private key and does not need to remain a secret. Public keys could be generated using the private key, however, it should not be possible to calculate the private key from the public key. The combination of the public key and the private key from your bitcoin wallet. The reason that public keys exist is in order to prove that a user knows the private key without revealing it to another person. In order to do that we use digital signatures.
A digital signature is a mathematical process of proving ownership of a private key without revealing it. The Elliptic Curve Digital Signature Algorithm, used in bitcoin, uses a finite field and an elliptic curve in order to sign transactions such that any user can prove authenticity of that signature without having to know the private key. There are three main cases of the ECDSA in Bitcoin:
- The signature will be a mathematical proof that the person who owns the bitcoin funds knows the private key and is authorized for a transaction to happen.
- It is impossible to later deny such a transaction, also known as ‘nonrepudiation’ in legal signatures.
- It is impossible to later modify a transaction after being signed.
I will delve into more detail about the process of digital signatures later, however let us understand elliptic curves and finite fields first.
Elliptic Curve
An elliptic curve is similar to normal equations we take in algebra. They are denoted as such, y²=x³+ax+b, where it’s discriminant Δ=4a³+27b² is not equal to 0. The main difference between an elliptic equation and a regular cubic equation is that the y term is squared, making an elliptic curve symmetrical along the x-axis (important point for what we will discuss soon).
Examples of invalid curves are ones that contain either cusps or self-intersections hence making the discriminant equal to 0. Examples:

Finite Fields
An elliptic curve could be defined over any field but when it comes to cryptography it is usually defined over finite fields.
A finite field is a predefined set of positive numbers and two operations, addition and multiplication, such that every calculation must fall in its range. Therefore if we had a number that goes beyond, the remaining would ‘wrap’ around.
We have two binary operations, addition and multiplication which follow modular arithmetic properties:
- Addition: (21+7) mod(19) = 9
- Subtraction: (9–15) mod(19) = 13
- Multiplication: (3*9) mod(19) = 8
- Additive inverse: (-8) mod(19) = 11
- Multiplication inverse (8^(-1))mod(19) = 12 (explanation: 8*x mod(19) = 1 where x=12)
In cryptography, the elliptic curve is defined over a finite field F of positive integers modulo p, where p is a prime number. In a finite field, a set of integers of modulo p consists of only integers from [0, p-1]. When an elliptic curve is defined over a finite field, both x and y coordinates of each point on the curve will be plotted in a square with sides of length p-1.
NOTE 1: it is important for p to be a prime number as for example a set of integers modulo 4 is not a field. The multiplicative inverse 2*x mod(4) = 1 has no solutions.
You could easily calculate whether a point belongs to an elliptic curve over a finite field. Any point (x, y) will belong to the curve if and only if it matches the following condition:
(x³ + 7- y²)(mod 17) = 0
For example the point (2, 7) belongs to the curve since (2³ + 7- 7²)(mod 17) = 0. However, the point (7, 9) does not belong on the curve since (7³ + 7- 9²)(mod 17) != 0.
Point Addition
The elliptic curve equation used in Bitcoin’s cryptography is called secp256k1 which uses this equation: y²=x³+7, a=0 b=7. As you can see in the below image, all y values are symmetric along the x-axis and only two possible y values exist for each x value.
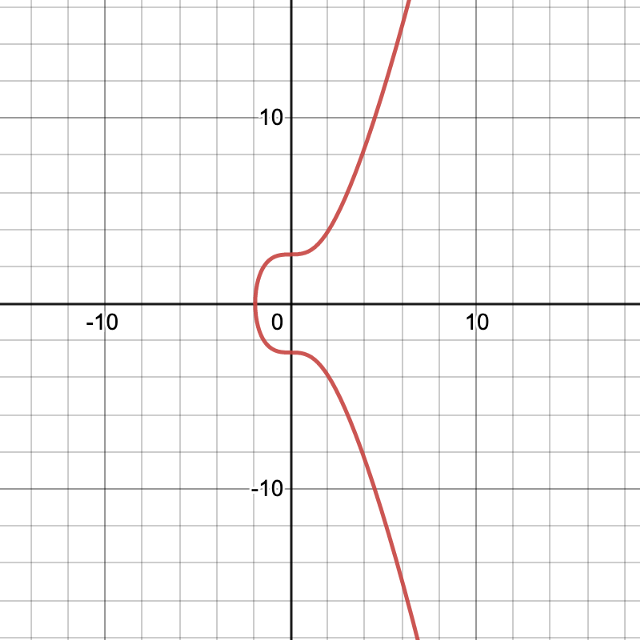
There are many important properties that elliptic curves have. Any line intersecting 2 non-tangent points on a curve will always intersect another third point. Also any line, non-vertical and tangent to the curve at a point, will always intersect another 1 (and only 1) point on the curve. This property is important for what we call point addition.
Point addition is useful for adding two points on a curve to get a third point on that curve. Say we have points A and B on an elliptic curve: A + B = C. The point addition of A and B will be the x-axis reflection of the third intersecting point, C’, of the line between A and B.
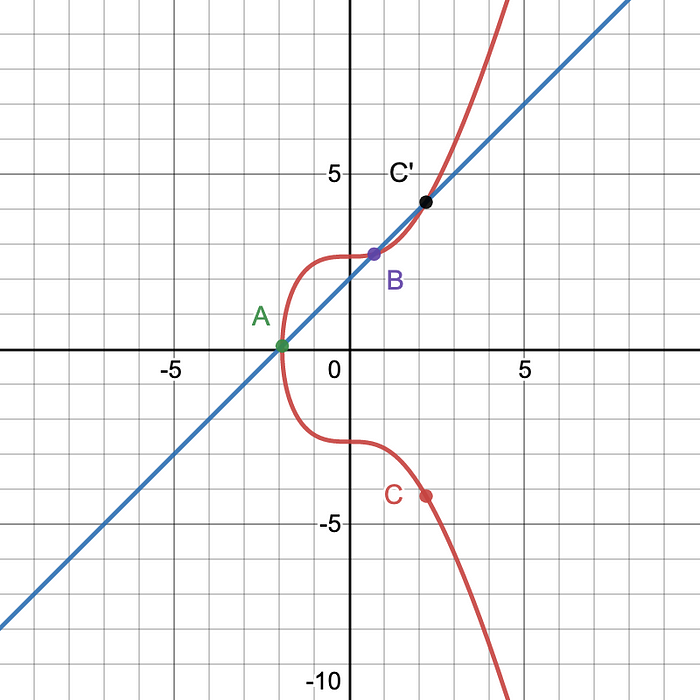
Similar situation in Figure 2. A + B = C.
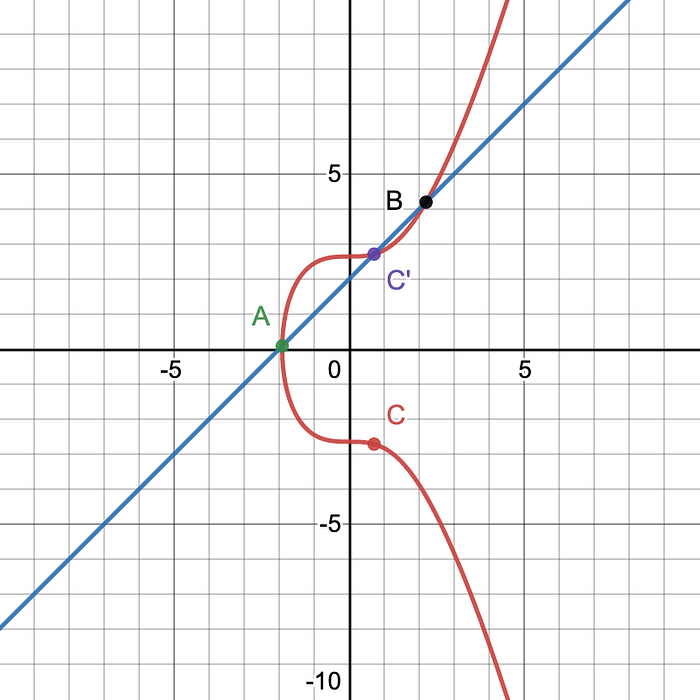
Multiplication
We just added two different points to each other. In order to add the same point to itself twice we find the line tangent to that point and then as mentioned before, the line will only intersect 1 other point, we take the reflection across the x-axis of the second point where the tangent line intersects on the curve.
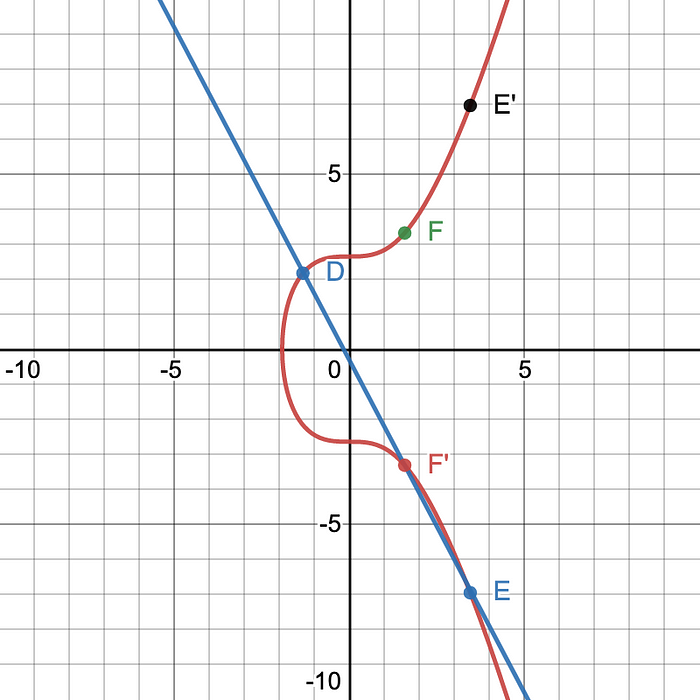
So say we have a line tangent to the point D and another point where that line intersects the curve called E’. Point doubling is similar to point addition except we could represent the tangent line as D + D = E where E is the reflection of the point E’ along the x-axis.
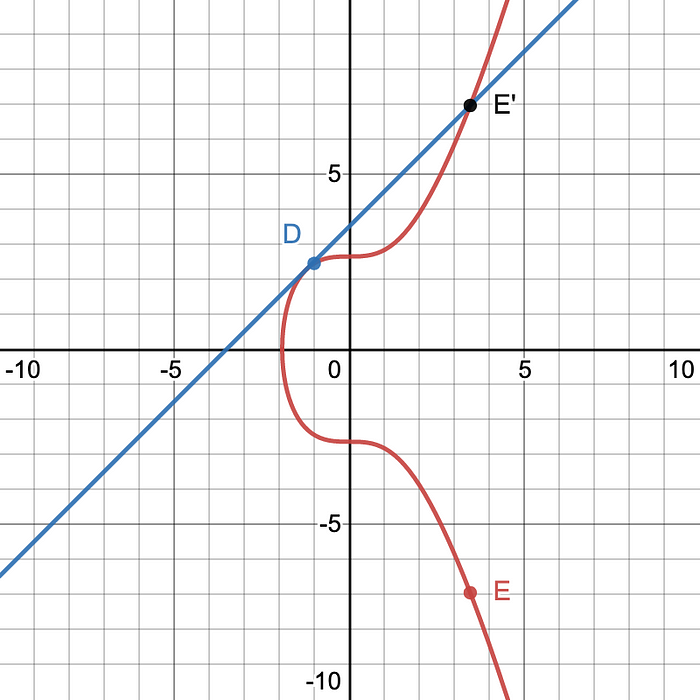
Another way this could be written is D+D=2·D. Therefore, if you want to find 3·D it would be the same as finding D+(D+D) or D+E which is similar to what was done earlier. As you can see in Figure 4, D+(D+D)=F
Order and Cofactor
An elliptic curve on a finite field forms a finite cyclic group containing all the points on that curve. The curve order is the total number of all points on the curve, while the subgroup order is the number of points in each cyclic subgroup.
For example take a curve y²=x³+2x+3 (mod 97) and a point P = (3, 6), we could use multiplication to calculate the multiples of P on the curve.
0P = 0
1P = (3, 6)
2P = (80, 10)
3P = (80, 87)
4P = (3, 91)
5P = 0
6P = (3, 6)
7P = (80, 10)
8P = (80, 87)
9P = (3, 91)
NOTE 2: In order to multiply a point D with any scalar n (n≥0) we could do it how we regularly do it, the product would be a repeated addition to itself or its multiplied self. However a faster way to do it for bigger n values is to represent n in its binary form and multiply D to it. For example, n=131071 it would be like this, (2¹⁶+2¹⁵+2¹⁴+2¹³+…+2³+2²+2¹+2⁰)·D. Therefore now instead of adding it 131071 times we just distribute these values and the binaries separately like this, (2¹⁶·D+2¹⁵·D+2¹⁴·D+…+2²·D+2¹·D+2⁰·D).
Then, in order to calculate the values of 2¹⁶·D and 2¹⁵·D… and so on, we do the following:
2·P = D + D
4·P = 2·D + 2·D
8·D = 4·D + 4·D
16·D = 8·D + 8·D
all the way to 2¹⁶ (65536).
As we could see there is a pattern of only 5 different multiples repeating cyclically. Therefore, adding multiples of P together will give you a multiple of P always being from one of the 5 points. Each set of multiples of P is what is referred to as a cyclic subgroup and point P is called the generator point (base point).
Depending on the curve, some form a single cyclic group (containing all the points), while others form several non-overlapping cyclic subgroups (each containing a subset of the curve’s points).
In curves with multiple cyclic groups, the points on the curve are split into h cyclic subgroups, each of order r where each subgroup contains an equal amount of points. The order of entire group, n, is defined as such: n = h * r (number of subgroups, h, multiplied by the amount of points in each subgroup, r).
Another name for the number of subgroups is cofactor. If a curve contains only one subgroup the cofactor = 1. For example, the secp256k1 curve used in Bitcoin has a cofactor = 1. For curves, such as the Curve25519, with more than one cyclic subgroup, the cofactor > 1.
Generator Point
As discussed briefly earlier, the predefined constant called the generator point G is used to generate any point in its same subgroup over the elliptic curve by multiplying G by an integer in the range of [0…r], r being the subgroup order (number of points in each subgroup; not the curve order).
Hence, all the possible elliptic curve points can be generated from the generator point. Also since there is only one subgroup for curves with cofactor = 1, the curve’s order n would be equal to r.
Different generator points generate different subgroups of points on the curve. It is important to note that in cryptography generator points are picked carefully in order to ensure the subgroup order is large enough. You could even have it be as large as the order of the curve.
For example, let’s take a curve similar to the one used in Bitcoin, y²=x³+7 (mod 17) with the generator point as G = (15, 13). If we multiply G by integers from [1, 18] (18, because 17+1), you would realize that there exists a cyclic subgroup order of 18 points. In other words, there is a pattern of only 18 different multiples repeating cyclically. Therefore the subgroup order r = 18, curve order is n = 18, and the cofactor is h = n / r = 18 / 18 = 1.
However, if we use the generator point as G = (12, 1) the subgroup order would be 6, curve order is n = 18, and the cofactor is h = n / r = 18 / 6= 3.
Now let’s learn why this is even important in cryptography!
Private and Public Keys
As discussed earlier, by multiplying a constant point G (generator point) by an integer k we get another point, P, on the elliptic curve Fp. Therefore in cryptography, you could use the integer k as the private key, P as the public key, and a specific point G as the generator. By P = k * G, we are able to generate public keys on the elliptic curve using any integer for the private key.
P = k * G:
- k — private key (integer)
- P — public key (point)
- G — generator point (point)
As described in NOTE 2 above, we are easily able to generate a public key with only a few calculations. For 256-bit curves, it would only take a few hundred calculations.
However, how is the private key considered to be private? If we have P and G, why can’t we find k?
Discrete Logarithm Problem
The elliptic curve discrete logarithm problem is the following computational problem: Given points P, G ∈ E(Fp) to find an integer k, if it exists, such that P= kG. This problem has been a prominent field of research in computational number theory and cryptography for several decades, and it is the essential building block for elliptic curve cryptography and pairing-based cryptography.
The discrete logarithm problem allows us to perform one-way calculations, giving us the ability to send information without having to worry about it being decrypted.
It is very easy and fast to calculate P = k * G, however for carefully chosen finite fields and elliptic curves, there does not exist any efficient solution to finding k due to the discrete logarithm problem.
For example, let’s use the curve y²=x³+2x+3 (mod 97) with G = (3, 6), and P = (80, 87) such that E(Fp) = {0, (3, 6), (80, 10), (80, 87), (3, 91)}. We are easily able to determine the value of k = 3 since P = 3G.
If E(Fp) has a relatively small order, it becomes way easier for attacking the discrete log problem on E. Therefore, for secure cryptography systems we need to select a generator point that will produce a high enough order value such that it does not cycle.
The secp256k1 Curve in Bitcoin
The curve used in Bitcoin’s public-key cryptography with the ECDSA algorithm is called secp256k1. The secp256k1 is an elliptic curve over a finite field with is equation written as such, y² mod p = (x³ + ax + b) mod p, using the following domain parameters:
- a (the constant “a” in y² ≡ x³ + a*x + b (mod p)) = 0x0000000000000000000000000000000000000000000000000000000000000000
- b (the constant “b” in y² ≡ x³ + a*x + b (mod p)) = 0x0000000000000000000000000000000000000000000000000000000000000007
- p (modulus) = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
- h (cofactor) = 1
- n (order; size; the count of all possible points) = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
- g (the curve generator point G (x, y)) = (0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798 , 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
The code below is an implementation of the secp256k1 in Python:
Elliptic Curve Digital Signatures Algorithm
In order to keep the private key ‘private’, there must be a way for people to verify that a person has access to that private key given the public key without revealing it.
Digital Signatures are very important in public key cryptography. Any type of message could be signed using the sender’s private key which could then be verified by anyone with the sender’s public key. The verification proves that the sender who owned that public key did have access to the private key. Hence, this process also verifies that the encrypted message, which is mathematically tied to the signature, has not been changed or messed with in any way. The verification process will fail if so.
The following is the process of the Elliptic Curve Digital Signatures Algorithm (ECDSA) used in Bitcoin.
Alice and Bob Want to Exchange
Say Alice wants to prove to Bob that she knows a specific secret number, x, but Bob cannot know what that number is. From Bob’s point of view, he needs to verify that Alice actually knows that secret number x and that she is not lying to him (keep in mind, he cannot actually know the number).
First of all we will select a point, D, on the elliptic curve called the base point known by both Alice and Bob.
After that Alice chooses the secret random number, x, and converts that secret number to a point by adding it x times to D and creating a new point X.
X = x·D
D = common point
x = secret random number
X = point generated
Due to asymmetry of point arithmetic as explained earlier, Bob cannot simply divide X by D to find x, making guessing the only option and therefore assuming Alice picked a really large x, it becomes impossible or inefficient to find it.
Therefore, Alice will send Bob another random number, equally as hard to guess, called r. She will also then add the two secret numbers together, x and r. It is important for r to remain a secret or else it would be possible to find x by subtraction.
b = x+r
r = secret random number
b = sum of the two secret numbers
The value b is essentially a secret similar to x, hidden in some random number r. Next, Alice also converts r to a point on the elliptic curve, called R, by adding D to itself r times,
R = r·D
R = point generated
Point R plays an important role in this process by giving just enough information about r without revealing it. Now Bob is given both b and R so that he is able to verify that Alice knows x. Therefore Bob takes the two points X and R and adds them together to generate a third point B.
B = X+R
B = point generated
Bob also converts b to a point called B’ (B prime) by doing the following,
B’ = b·D
B’ = point generated
Therefore by checking that B and B’ are equal Bob is able to verify that Alice knows x also while maintaining its secrecy. However, we have a problem as that allows Alice to cheat…
The Problem that Allows Alice to Cheat
Since Alice knows that Bob will be adding X and R together to find point B, she could use a fake x value and use that to create point X. Then she will subtract the point X from point R,
R = r·D-X
Then after that Bob will be continuing the same process as explained earlier and adding X and R together. In that case, when he tries to find B the two X’s will cancel out,
B = X + R
B = X + r·D-X
B = r·D
Alice could then sets b equal to r without knowing x and therefore it would satisfy the proof,
b = r
B = r·D
B’ = b·D = r·D
B = B’
Bob thinks that he verified since B and B’ but was instead fooled by Alice. This would not be a secure system but there is a solution!
The Solution
In the above process, Bob added X to R only once but instead he will now be adding X multiple times, calling this number m which should be a very large unpredictable number.
B = m·X+R
It is really important that Bob chooses m only after Alice sends him the point R. The reason that m needs to be an unpredictable number is to prevent Alice from canceling out the X from R. Therefore, multiplying it by an unpredictable number. Alice won’t be sent the value of m until she has chosen the value of r and sent the point R.
However in cryptography, there is a way to make this system more efficient and prevent more interaction between Alice and Bob. Instead of using a random value for m specified by Bob which needs to be later sent to Alice, the hash of R is used for the value of m. In this case the value of m will not be predictable until the value of R is specified by Alice.
In order to make a signature from the proof and make sure that a signature for one message could not be reused for a different message, Alice will need to customize a hash function with a message that she is signing.
m = hash(R)
By using the value of m·X Alice will not be able to cancel it out from R as she would to try an insanely large amount of times (2²⁵⁶ if using the SHA256 function) in order to find the value of m which will satisfy R = r·D-m·X.
Finally, the process would go like this:
- Alice will choose the secret value r then send Bob R=r·D.
- Uses a hash function to get a random “challenge” m:= Hash( R ).
- Computes b := m·x + r.
- Alice sends point R and number m to Bob who verifies that m·D equals R + m·X.
- Alice customizes a hash function with a message that she is signing.
Thank You for Reading
If you enjoyed this article, you could follow me on Medium and Twitter @suhailsaqan.